前言

理解红黑树需要掌握下面知识

  • 二分查找算法
  • 二叉查找树
  • 自平衡树（AVL树和红黑树）

基于二分算法设计出了二叉查找树，为了弥补二叉查找树倾斜缺点，又出现了一些自平衡树，比如AVL树，红黑树等。

二分查找算法

在40亿数据中查找一个指定数据最多只需要32次，这就是二分查找算法的魅力。

二分查找算法（又叫折半查找算法）是一种在有序数组中查找某一特定元素的搜索算法。注意有序数组的前提。

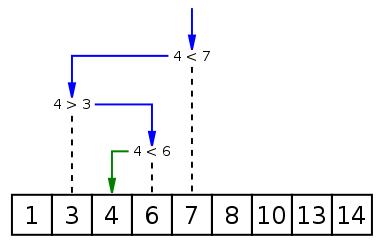
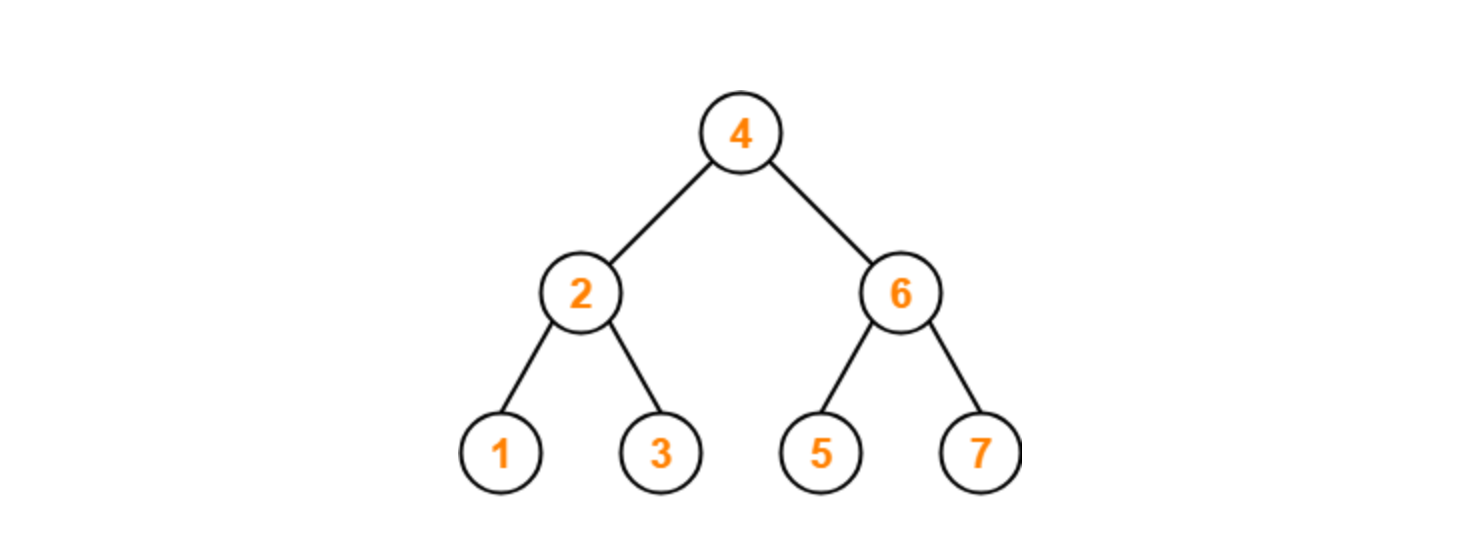
下图中查找 4 ，查找从中间元素开始 4 < 7 ，从左边查找 4 > 3 ，从右边查找 4 < 6，然后找到元素。

Binary_search_into_array

二分查找算法时间和空间复杂度，$n$ 是数组长度。

平均时间复杂度 ${O(\log n)}$

最坏时间复杂度 ${O(\log n)}$

最优时间复杂度 ${O(1)}$

循环空间复杂度 ${O(1)}$

递归空间复杂度 $O(log n)$

Java 递归实现二分查找。

    public static int binarySearch(int[] arr, int start, int end, int hkey) {
        if (start > end) {
            return -1;
        }
        int mid = start + (end - start) / 2;    //防止溢位
        if (arr[mid] > hkey) {
            return binarySearch(arr, start, mid - 1, hkey);
        }
        if (arr[mid] < hkey) {
            return binarySearch(arr, mid + 1, end, hkey);
        }
        return mid;
    }

Java 循环实现二分查找。

    public static int binarySearch(int[] arr, int start, int end, int hkey) {
        int result = -1;
        while (start <= end) {
            int mid = start + (end - start) / 2;    //防止溢位
            if (arr[mid] > hkey) {
                end = mid - 1;
            } else if (arr[mid] < hkey) {
                start = mid + 1;
            } else {
                result = mid;
                break;
            }
        }
        return result;
    }

二叉查找树

二叉查找树（Binary Search Tree，简称BST）是一棵二叉树，它具有以下性质：

  1. 若任意节点的左子树不空，则左子树上所有节点的值都小于它的根节点的值；
  2. 若任意节点的右子树不空，则右子树上所有节点的值都大于它的根节点的值；
  3. 任意节点的左、右子树也分别为二叉查找树。

二叉树：每个节点最多只有两个分支，分别称为“左子树”或“右子树”。

二叉查找树操作（搜索，插入，删除）效率依赖树高度。

最坏情况，树向一边倾斜，树高度 $n$ （节点数量），此时操作时间复杂度为 $O(n)$

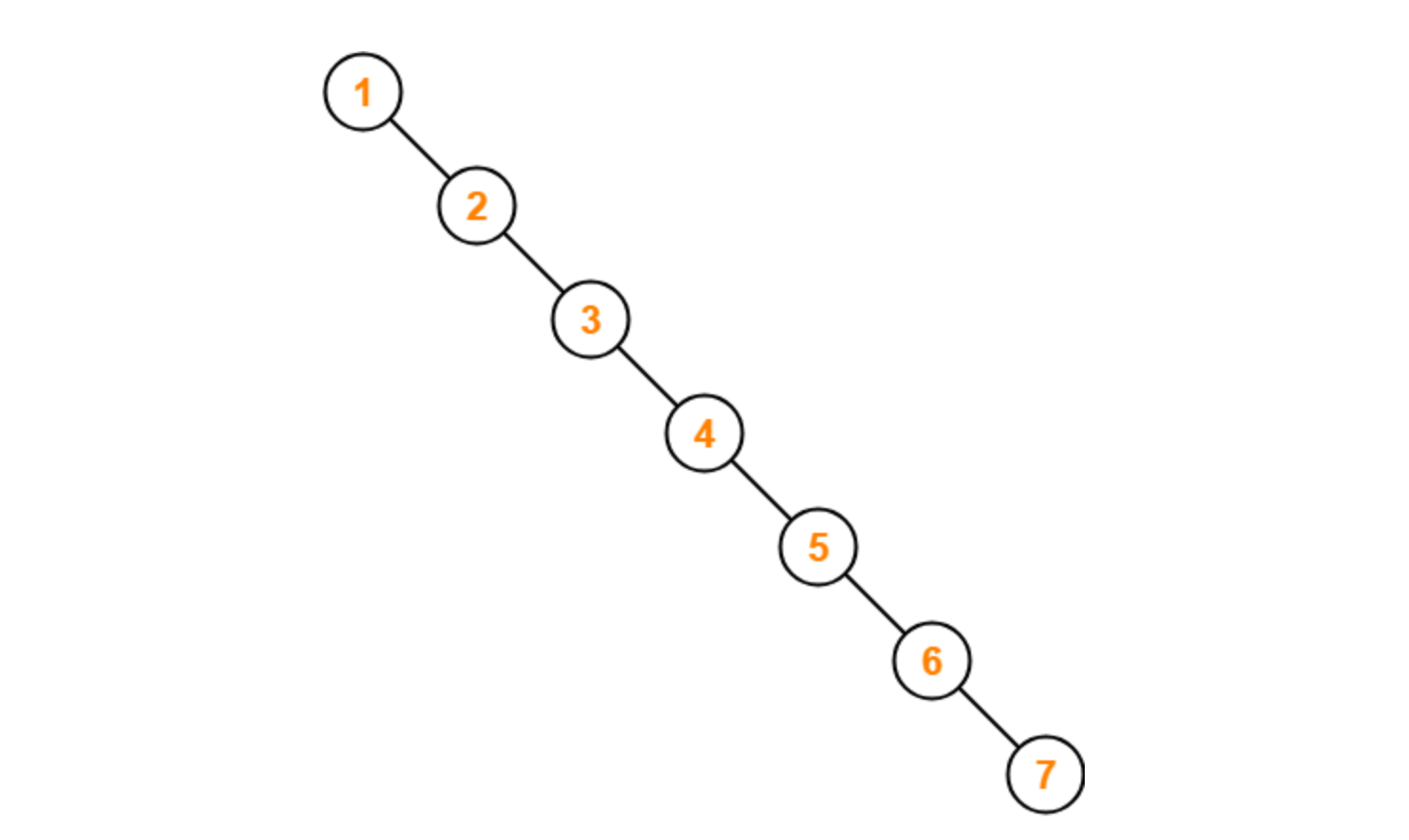
image-20211116181348525

理想情况，树高度 $log(n)$ ，操作时间复杂度 $O(log(n))$ ，此时它是一棵平衡的二叉查找树。

image-20211116181414324

算法 平均 最差
空间 O(n) O(n)
搜索 O(log n) O(n)
插入 O(log n) O(n)
删除 O(log n) O(n)

为了让二叉查找树尽可能达到理想情况，出现了一些自平衡二叉查找树，如AVL树和红黑树。

AVL树

AVL树中的每个节点都有一个平衡因子属性（左子树高度减去右子树高度）。每次元素插入删除操作后，会重新进行平衡计算，如果节点平衡因子不为 [1,0,-1] 时，需要通过旋转使树到达平衡。AVL 树中有 4 种旋转操作。

  1. 左旋（Left Rotation）
  2. 右旋（RightRotation）
  3. 左右旋转（Left-Right Rotation）
  4. 左右旋转（Right-Left Rotation）

AVL_Tree_Example

下面是 Java AVL 树的例子

    private Node insert(Node node, int key) {
      	.....
        return rebalance(node); // 重新平衡计算
    }

    private Node delete(Node node, int key) {
      	.....
        node = rebalance(node); // 重新平衡计算
        return node;
    }

		private Node rebalance(Node z) {
        updateHeight(z);
        int balance = getBalance(z);
        if (balance > 1) {
            if (height(z.right.right) > height(z.right.left)) {
                z = rotateLeft(z);
            } else {
                z.right = rotateRight(z.right);
                z = rotateLeft(z);
            }
        } else if (balance < -1) {
            if (height(z.left.left) > height(z.left.right)) {
                z = rotateRight(z);
            } else {
                z.left = rotateLeft(z.left);
                z = rotateRight(z);
            }
        }
        return z;
    }

https://github.com/eugenp/tutorials/blob/master/data-structures/src/main/java/com/baeldung/avltree/AVLTree.java

红黑树

性质

红黑树中的每个节点都有一个颜色属性。每次元素插入删除操作后，会进行重新着色和旋转达到平衡。

红黑树属于二叉查找树，它包含二叉查找树性质，同时还包含以下性质：

  1. 每个节点要么是黑色，要么是红色。
  2. 所有的叶子节点（NIL）被认为是黑色的。
  3. 每个红色节点的两个子节点一定都是黑色（不会出现两个连续红色节点）。
  4. 从根到叶子节点（NIL）的每条路径都包含相同数量的黑色节点。

Red-black_tree_example

查找

查找不会破坏树的平衡，逻辑也比较简单，通常有以下几个步骤。

  1. 从根节点开始查找，把根节点设置为当前节点；
  2. 当前节点为空，返回null；
  3. 当前节点不为空，查找key小于当前节点key，左子节点设为当前节点。
  4. 当前节点不为空，查找key大于当前节点key，右子节点设为当前节点。
  5. 当前节点不为空，查找key等于当前节点key，返回当前节点。

代码实现可以参考 Java 里面的 TreeMap。

	Entry<K,V> p = root;
	while (p != null) {
		int cmp = k.compareTo(p.key);
		if (cmp < 0){
			p = p.left;
    }else if (cmp > 0){
      p = p.right;
    }else{
      	return p;
    }
  }
	return null;

插入

插入操作分两大块：一查找插入位置；二插入后自平衡。

  1. 将根节点赋给当前节点，循环查找插入位置的节点；
  2. 当查找key等于当前节点key，更新节点存储的值，返回；
  3. 当查找key小于当前节点key，把当前节点的左子节点设置为当前节点；
  4. 当查找key大于当前节点key，把当前节点的右子节点设置为当前节点；
  5. 循环结束后，构造新节点作为当前节点左(右)子节点；
  6. 通过旋转变色进行自平衡。

代码实现可以参考 Java 里面的 TreeMap。

	Entry<K,V> t = root;
  Entry<K,V> parent;
	int cmp;
	do {
		parent = t;
		cmp = k.compareTo(t.key);
    if (cmp < 0){
			t = t.left; 
    }else if (cmp > 0){
			t = t.right;
    }else {
			return t.setValue(value);   // 更新节点的值，返回
    }
  } while (t != null);

	Entry<K,V> e = new Entry<>(key, value, parent);
		if (cmp < 0){
		  parent.left = e;
		}else {
			parent.right = e;  
	}
  fixAfterInsertion(e); // 通过旋转变色自平衡

插入场景分析

  1. 根节点为空，将插入节点设置为根节点并设置为黑色；
  2. 插入节点的key已存在，只需要更新插入值，无需再自平衡；
  3. 插入节点的父节点为黑色，直接插入，无需自平衡；
  4. 插入节点的父节点为红色。

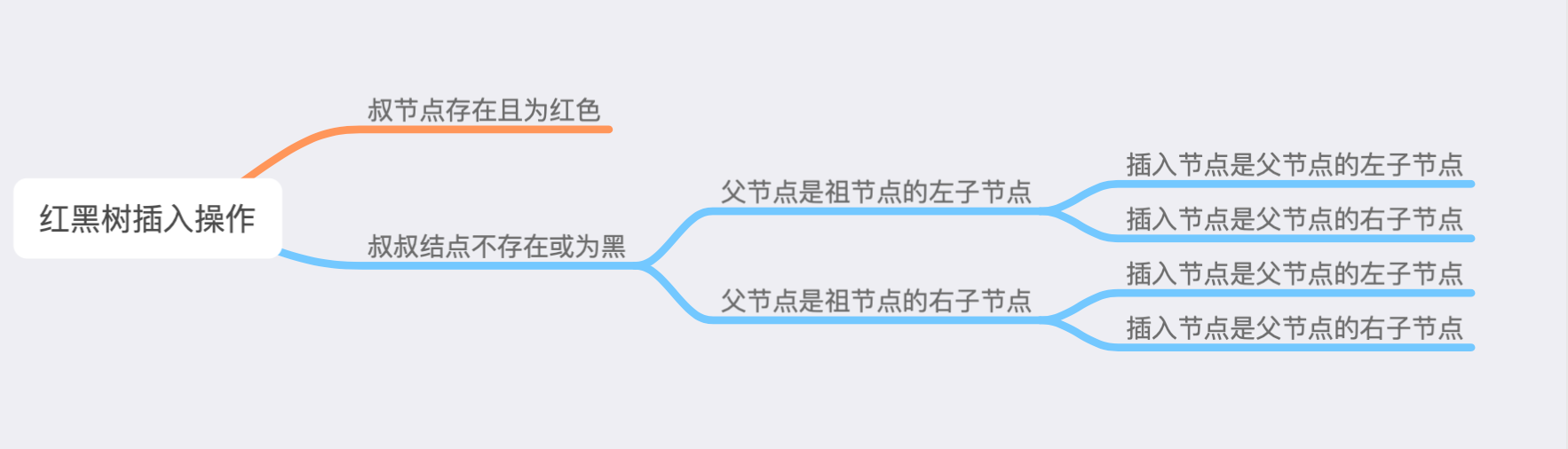
场景 4 插入节点后出现两个连续的红色节点，所以需要重新着色和旋转。这里面又有很多种情况，具体看下面。

先声明下节点关系，祖节点（10），叔节点（20），父节点（9），插入节点（8）。

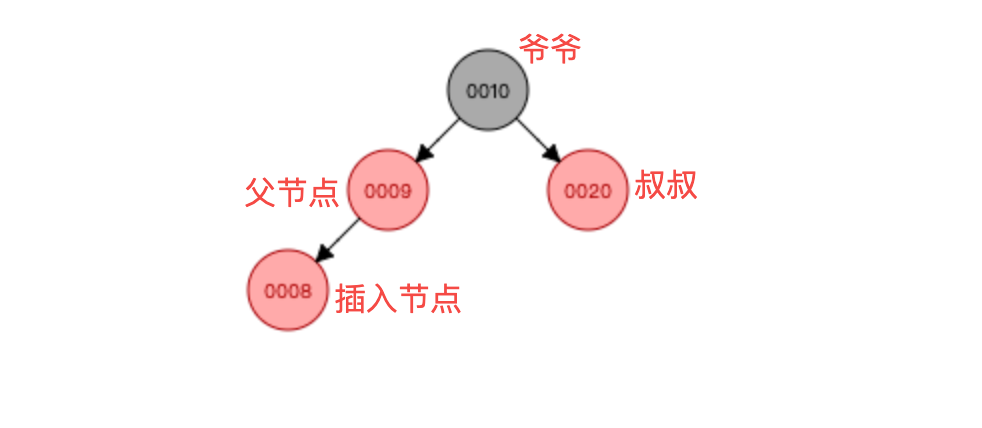
image-20211118154701421

一般通过判断插入节点的叔节点来确定合适的平衡操作。

image-20211119170210130

叔叔节点存在且为红色。

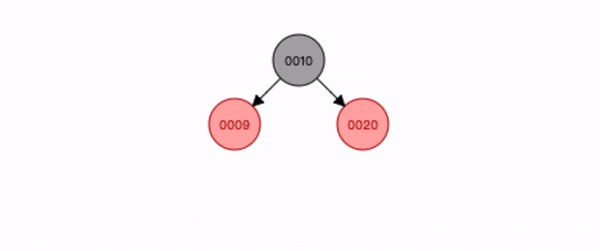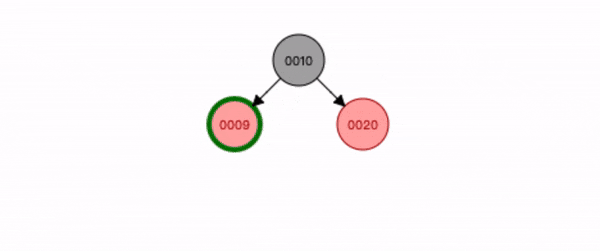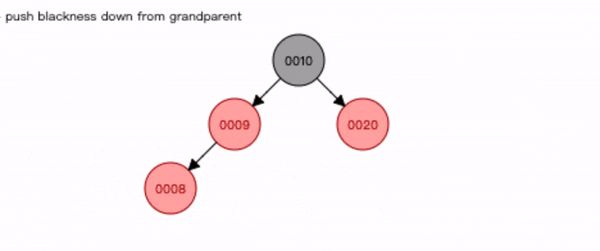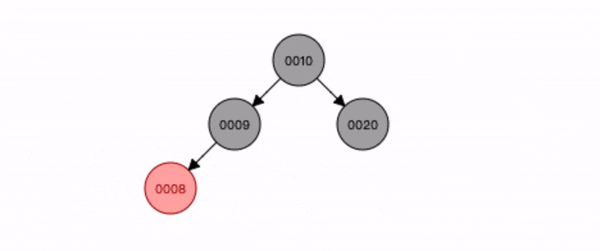
rb_insert_01

  1. 先查找位置将**节点8 **插入；
  2. 将**父节点9 和叔节点20 **变为黑色，祖节点10 变为红色；
  3. 祖节点10 是根节点，所以又变为黑色。

叔叔节点不存在或为黑色，父节点是祖节点的左节点，插入节点是父节点的左子节点。

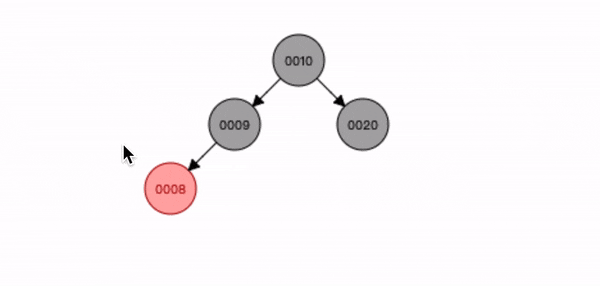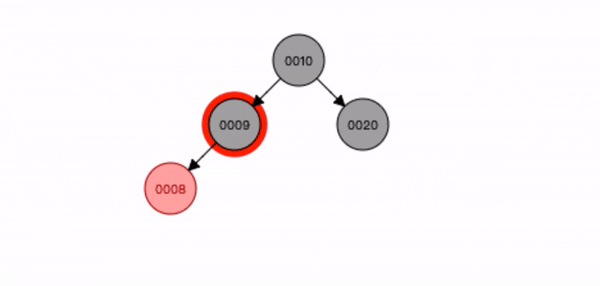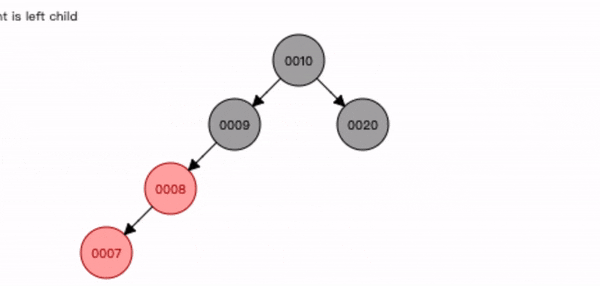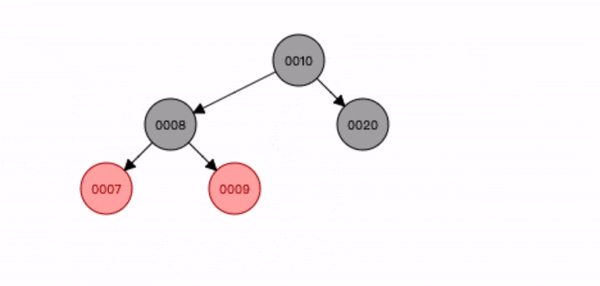
rb_insert_02

  1. 先查找位置将节点7 插入；
  2. 将祖节点9 进行右旋转；
  3. 将父节点8 变为黑色，祖节点9 变为红色；

叔叔节点不存在或为黑色，父节点是祖节点的左节点，插入节点是父节点的右子节点。

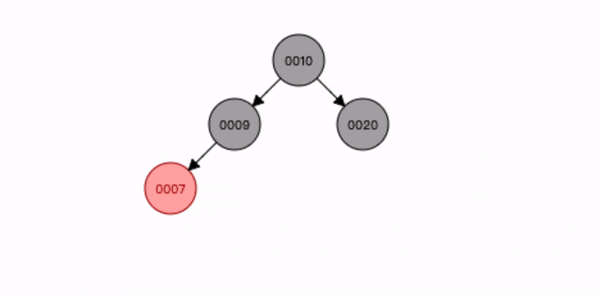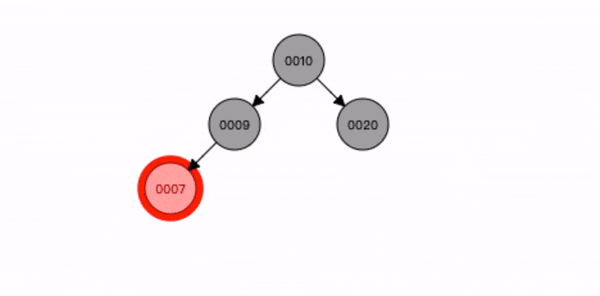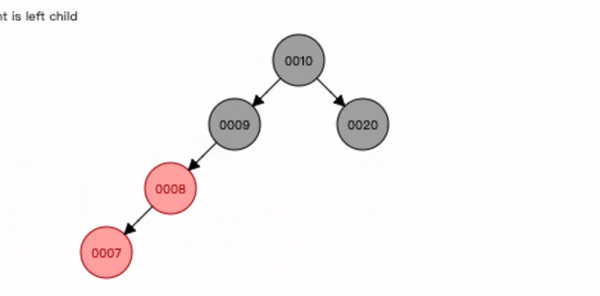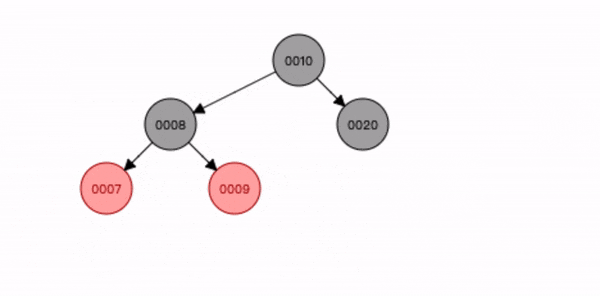
rb_insert_03

  1. 先查找位置将节点8 插入；
  2. 将父节点7 进行左旋转；
  3. 将祖节点9 进行右旋转；
  4. 将插入节点8 变为黑色，祖节点9 变为红色；

叔叔节点不存在或为黑色，父节点是祖节点的右节点，插入节点是父节点的右子节点。

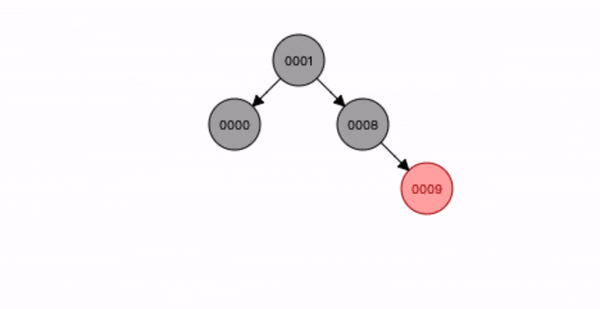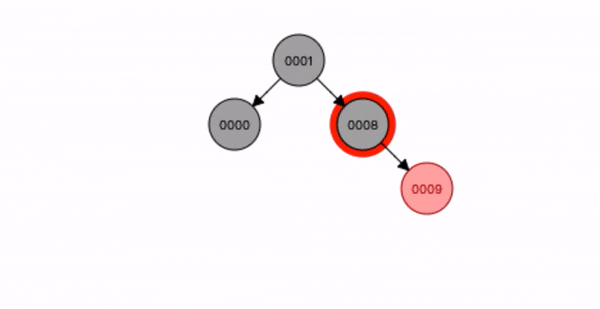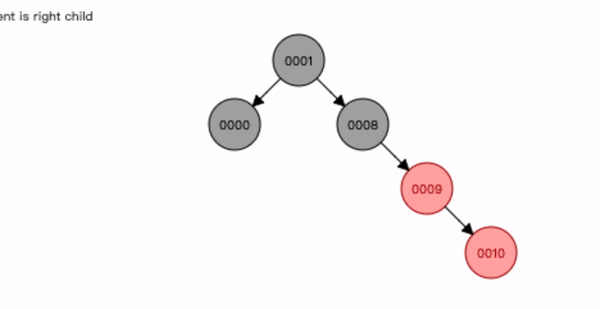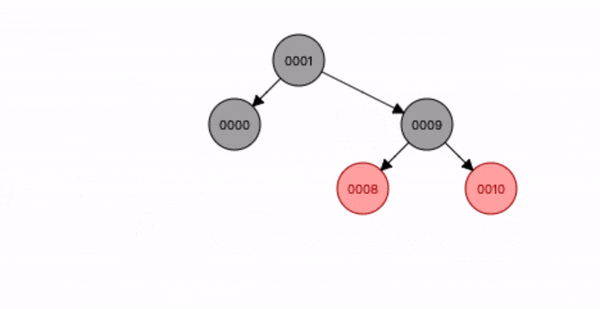
rb_insert_04

  1. 先查找位置将节点9 插入；
  2. 将祖节点8 进行左旋转；
  3. 将父节点9 变为黑色，祖节点8 变为红色；

叔叔节点不存在或为黑色，父节点是祖节点的右节点，插入节点是父节点的左子节点。

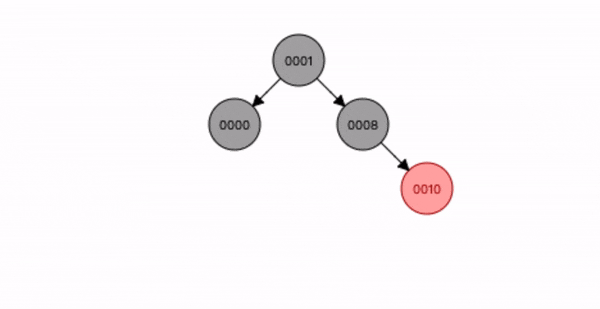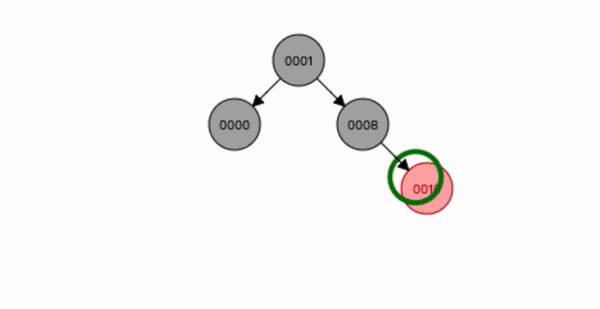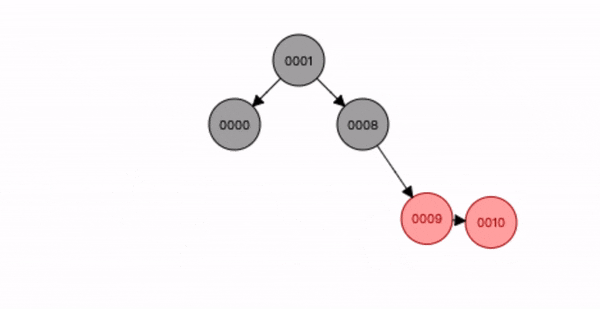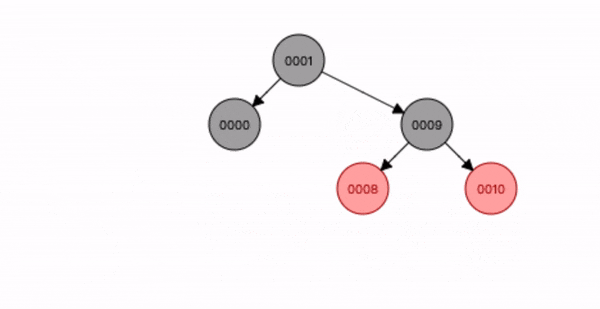
rb_insert_05

  1. 先查找位置将节点9 插入；
  2. 将父节点10 进行右旋转；
  3. 将祖节点8 进行左旋转；
  4. 将插入节点9 变为黑色，祖节点8 变为红色；

删除

删除操作分两大块：一查找节点删除；二删除后自平衡。删除节点后需要找节点来替代删除的位置。

根据二叉查找树性质，删除节点之后，可以用左子树中的最大值或右子树中的最小值来替换删除节点。如果删除的节点无子节点，可以直接删除，无需替换；如果只有一个子节点，就用这个子节点替换。

思考一些删除场景，使用下面可视化工具模拟场景。

https://www.cs.csubak.edu/~msarr/visualizations/RedBlack.html

替换节点和删除节点其中一个红色

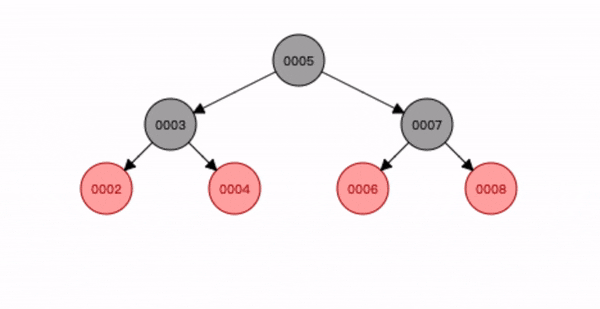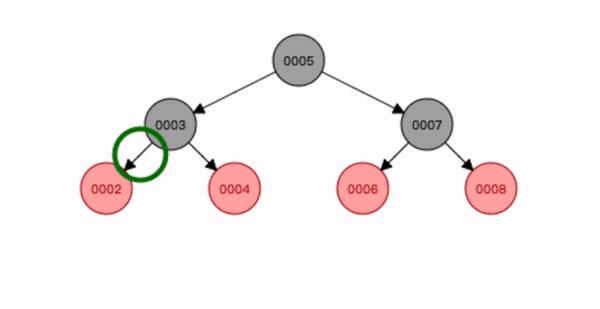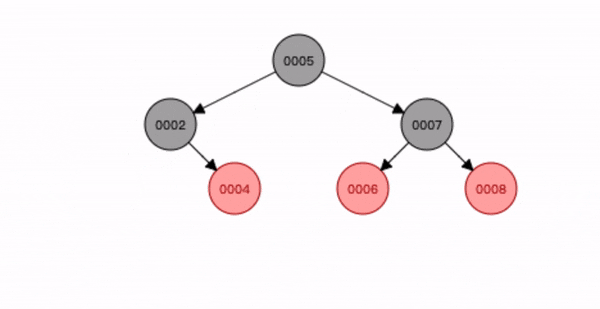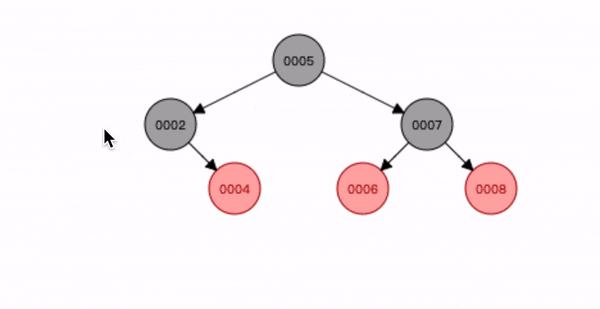
rb_del_01

  1. 查找到删除节点3，将它删除；
  2. 节点2 替换删除位置，并变为删除节点3 的黑色。

替换节点和删除节点都是黑色，它兄弟节点是黑色，兄弟节点的子节点至少有一个红色。

替换节点和删除节点都是黑色，它兄弟节点是黑色，兄弟节点的子节点至少有一个红色。

替换节点和删除节点都是黑色，它兄弟节点是黑色，兄弟节点的两个子节点都是黑色。

替换节点和删除节点都是黑色，它兄弟节点是红色。

AVL树和红黑树对比

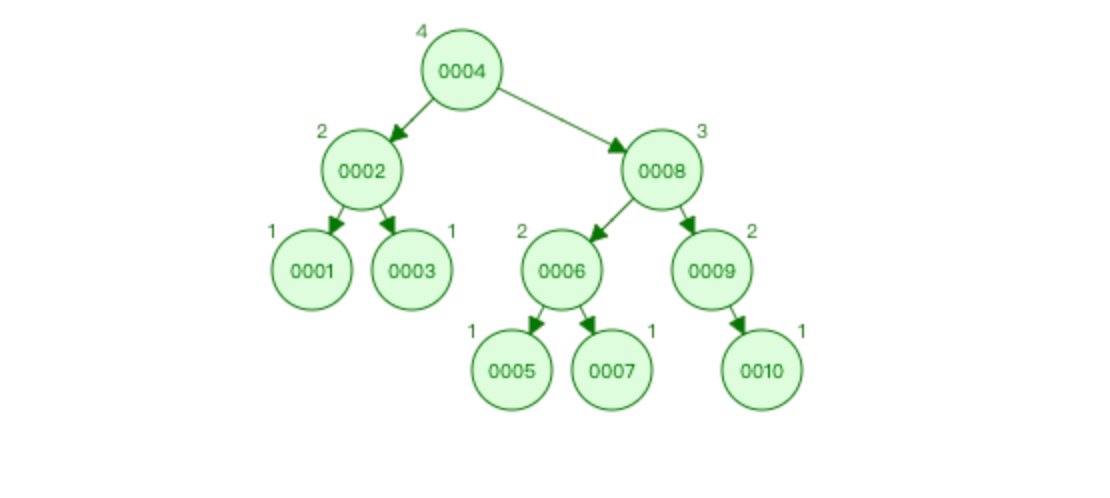
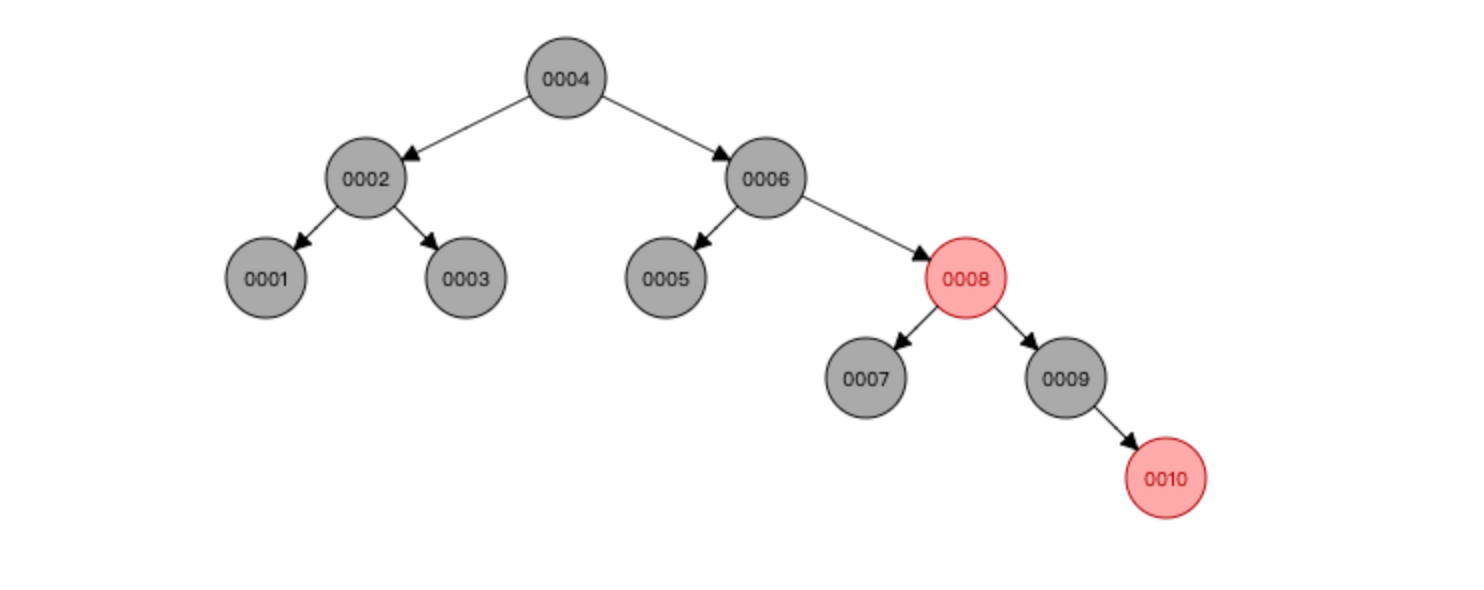
下面是[1-10]分别存储在AVL树和红黑树的图片。可以看出：

  • AVL树更严格平衡，带来查询速度快。为了维护严格的平衡，需要付出频繁旋转的性能代价。
  • 红黑树相较于要求严格的AVL树来说，它的旋转次数少。

image-20211118194355014

image-20211118194424425