B-tree

介绍

B-tree（平衡多路查找树）是自平衡树的数据结构，维护已排序的数据。关于二叉树和其它自平衡树可查看上篇红黑树。

一棵 $m$ 阶的树满足以下性质，

  1. 每个节点最多有$m$个子节点。

  2. 如果根不是叶节点，则根至少有两个子节点。

  3. 每个非叶节点（根除外）至少有 [$\frac{m}{2}$] 个子节点。

  4. 具有 $k$ 个子节点的非叶节点包含 $k-1$ 个键。

  5. 所有的叶子节点都具有相同的高度。

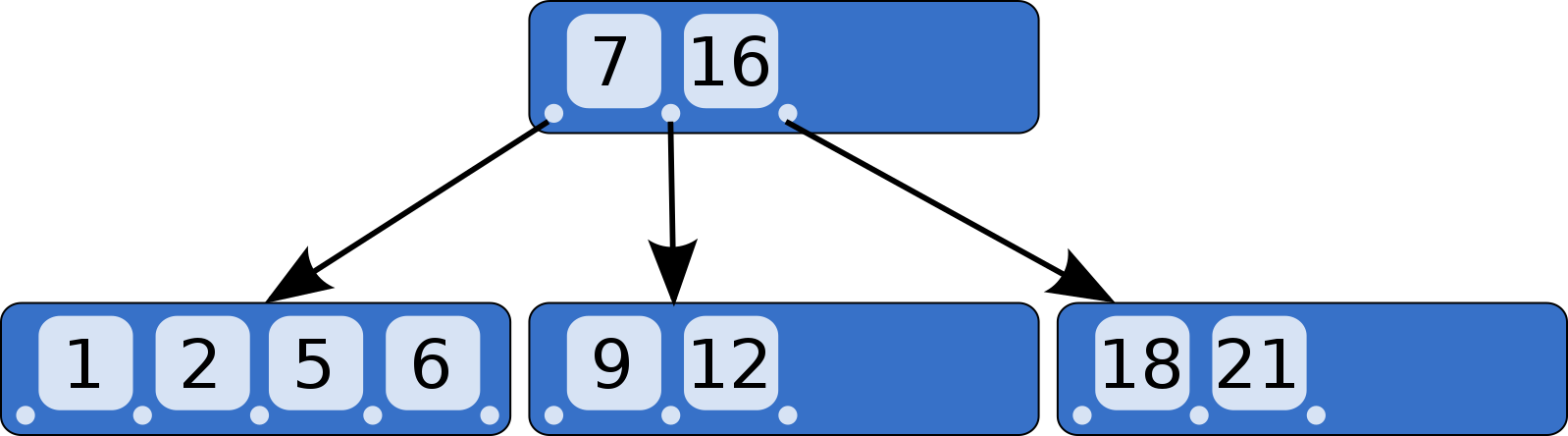
每个非内部节点的键充当分隔其子树的分隔值。例如，下面是一棵 5 阶树的片段，内部节点有包含两个键 [7, 16] ，所以它有三个子节点，最左边子节点的键满足小于7，中间子节点的键满足大于7小于16，最右边子节点的键满足大于于16。

内部节点：内部节点是除叶节点和根节点之外的所有节点。

5_B-tree

场景

B-tree 跟 红黑树应用场景不同，这种数据结构是为了处理大量数据而发明，它针对读写大数据量系统进行优化，常用于数据库和文件系统。

红黑树常用在应用程序，因为它处理的数据量一般不超过主存(RAM)容量。在数据库场景中，数据量都是GB，TB级别，数据存储在磁盘上，每次操作需要访问磁盘读取数据。

计算机存储硬件中访问数据的时间从快到慢依次如下：

  • 寄存器
  • CPU缓存（L1、L2 和 L3）
  • 主内存（RAM）
  • 磁盘驱动器（固态磁盘）
  • 磁盘驱动器（磁盘）
执行典型指令   　　　　　　　　　　   1/1000000000 秒 = 1纳秒
从一级缓存中读取数据 　　　 　　　　   0.5 纳秒
从二级缓存中读取数据 　　　　　　　    7 纳秒
从主内存中读取数据 　　  　　　　 	   100 纳秒 
从新的磁盘位置读取数据 　　  				8000000 纳秒 = 8毫秒

从上面可以看出，主内存的访问时间在纳秒级别，磁盘访问时间在毫秒级别。这意味着如果程序从磁盘读取会比从主内存读取慢 100, 000 倍。

所以 B-tree 优化目的就是减少磁盘访问次数，通过下面方式：

  • 降低树高度，使用多叉树结构，让单个节点存储更多个键。
  • 数据以块读取，这样一次可以读取更多数据，一般来说节点容量等于磁盘块大小。

1秒=1000毫秒=1000000微秒=1000000000纳秒

自平衡

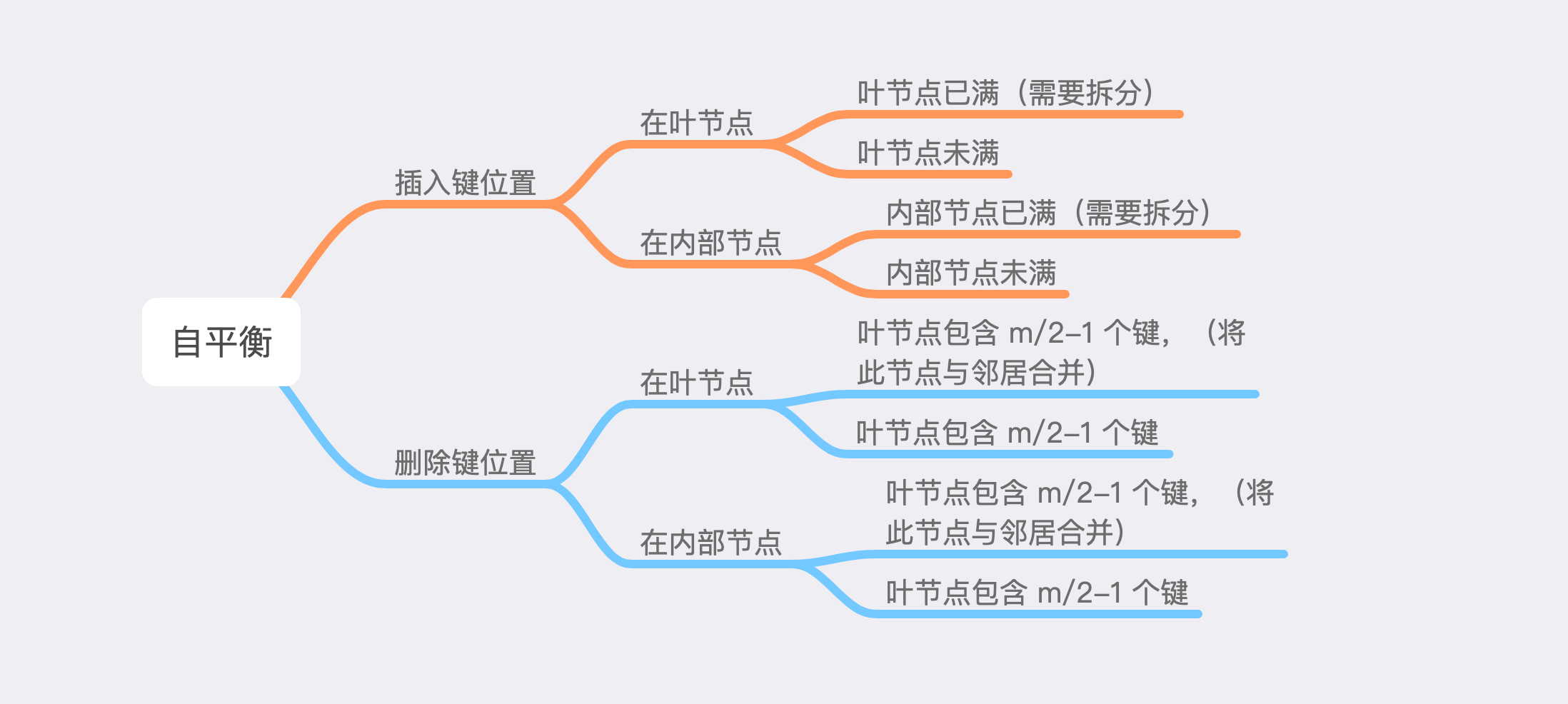
image-20211125153852383

拆分树节点

下面是一个 6阶B-tree（m=6），它一个节点可以拥有的最大键数是5，当插入数字6时，左边节点到达最大键，需要拆分树的节点。

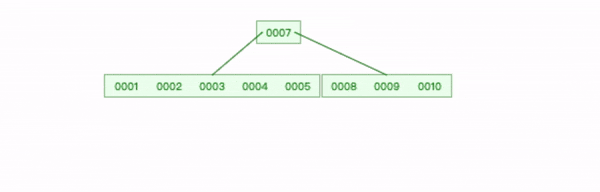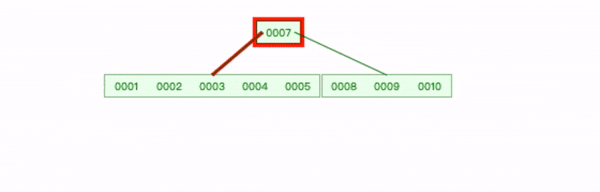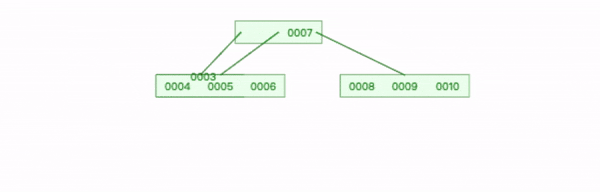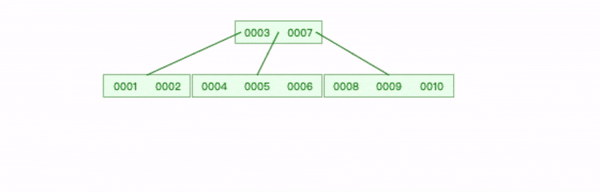
btree-insert

插入新数字6 步骤如下：

  1. 先求出节点的中位数为 3；

  2. 创建一个新的叶节点，将中位数 3 之后的所有键复制到新节点；

  3. 将中位数3 上移，插入到父节点适当位置；

  4. 在中位数3 后添加一个父节点到新节点的指针；

  5. 将新数字 6 添加到新节点的正确位置。

合并树的两个节点

删除键后，如果节点键数量小于最小键数时需要合并节点。下面树一个节点可以拥有的最小键数为2。

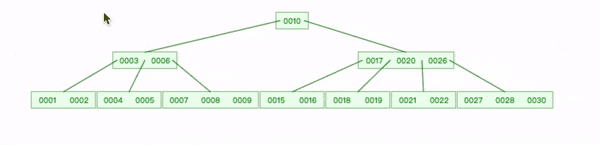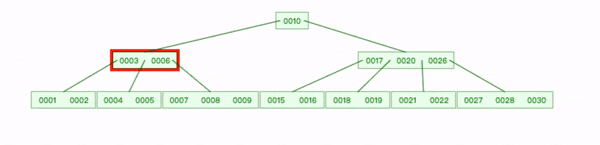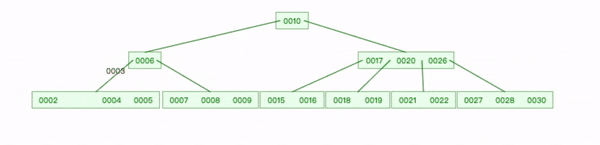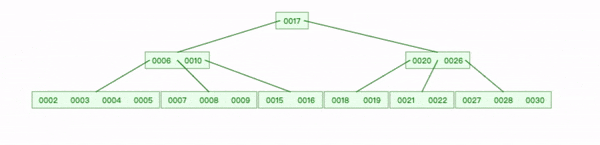
btree-del

删除叶节点键1：

  1. 查找到1删除；
  2. 删除3左指针，将 2 复制到 [4，5]节点，3下移；
  3. 3下移后，只有一个键6，父节点继续下移，直到平衡。

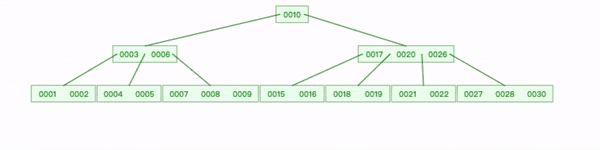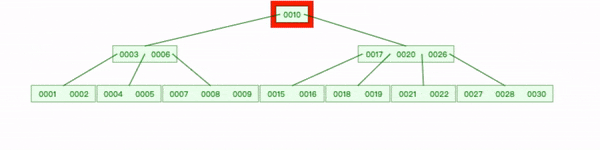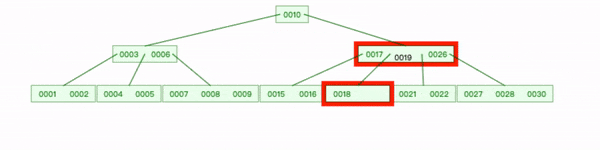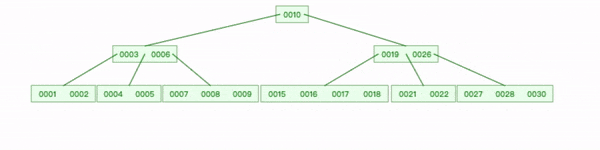
btree-del2

删除内部节点20：

  1. 查找到 20 删除，选取 20位置左子节点中最大值19 替换；
  2. 删除 19位置左指针；
  3. 17 键下移到 [15,16]节点，18追加到后面。

B+tree

B+tree 是 B-tree 一个优化版本，用于数据库索引。B+tree与B-tree的区别主要有两个方面：

  • B+tree非叶子节点只存储键，而B-tree所有节点都可以存储键值；

  • B+tree 键对应的值都存储在叶节点并且通过链表链接在一起。

下图展示了B+tree存储键值的情况，键 [1-7] 对应的值 [d1-d7]。

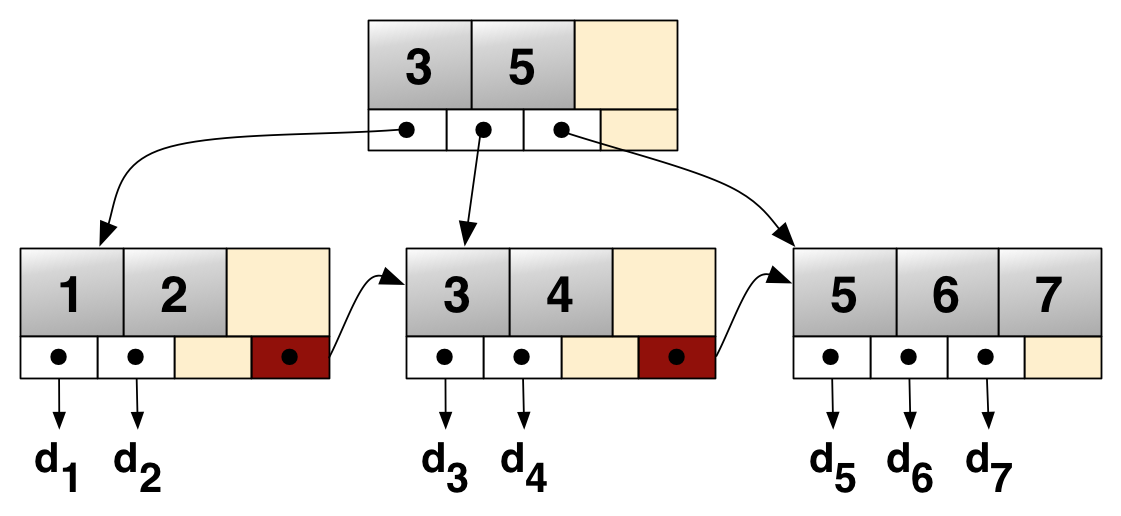
Bplustree

MySQL存储引擎 InnoDB中的 B+tree

MySQL 创建表时会生成一个 .ibd文件，这个ibd文件是一个功能齐全的空间。每个空间又被拆分成多个页面(Page)，每一页都会分配了一个 32 位整数页号，每个页面大小通常为16kB。

B+tree 索引中每个节点容量一个页面的大小，叶子节点和非叶子节点数据类型不同。

叶子节点包含键值和下一条记录的指针。

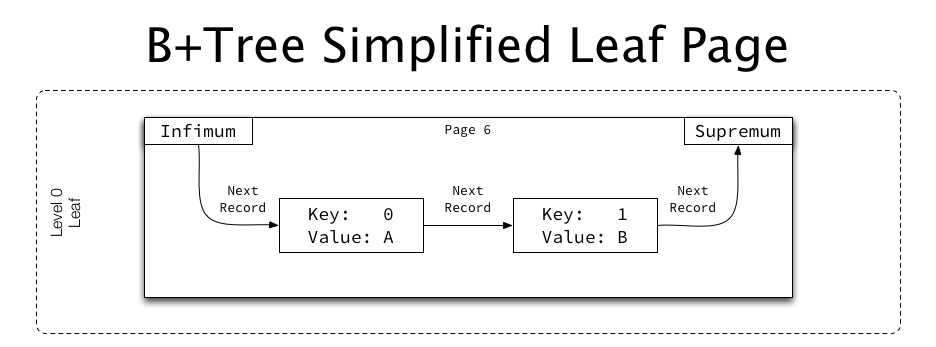
B_Tree_Simplified_Leaf_Page

非叶子节点包含子页面的页码和指向的子页面的最小键。

B_Tree_Simplified_Non_Leaf_Page

同级节点之间，每个节点上一页和下一页的指针，形成同一级别页面的双向链表。

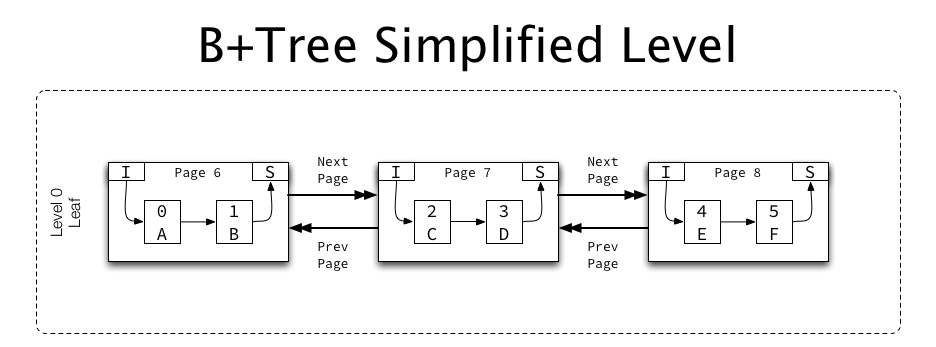
B_Tree_Simplified_Level

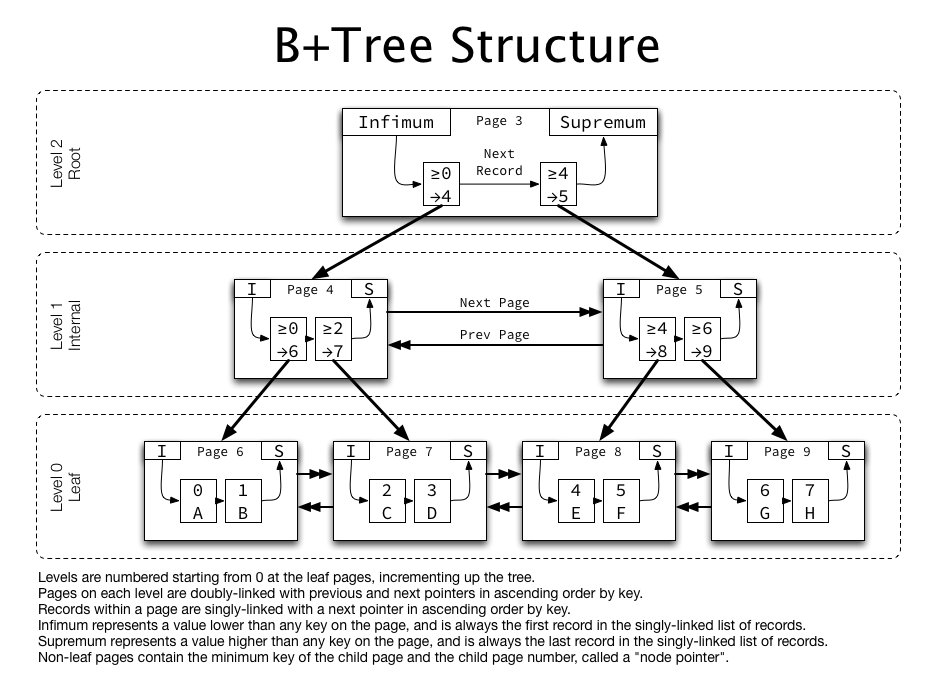
综上索引结构如下，同级页面形成双向链接，在每个页面内记录升序链接，非叶页面包含子页面“指针”（子页码）。

B_Tree_Structure

关于B+tree 效率问题，可以查看下表

树高度 非叶页面 叶子页面 行数 大小
1 0 1 468 16.0 KB
2 1 1203 > 56.3 万 18.8 MB
3 1204 1447209 > 6.77 亿 22.1 GB
4 1448413 1740992427 > 8140 亿 25.9 TB

大多数表索引高度再1-3级，所以一般只需要1-3次磁盘IO操作就可以完成。上面图中描述的都是聚集索引（主键）。

数据库中的 B+Tree索引分为聚集索引（clustered index）和次要索引（secondary index），聚集索引的叶子页是包含整行数据的页面，次要索引的叶子页存储了对应行的主键。

  • 使用聚集索引查询可以直接获得整行数据。
  • 使用次要索引查询时，先查询到主键值，然后再通过主键在聚集索引中找到完整的行数据。

小结

B-tree 是一种大数据量场景下的优化数据结构，旨在减少磁盘访问次数（降低树高度）。

B-tree 中的著名版本 B+tree 通过让非叶节点只存储键，占用空间变小，使得每一层节点可以索引更多数据，有效控制了树高度。

MYSQL的InnoDB中使用 B+tree 作为索引，正常情况下树高度保持在 1-4 级。