简介

数据结构（英语：data structure）是计算机中存储、组织数据的方式。

数据结构是一种具有一定逻辑关系，在计算机中应用某种存储结构，并且封装了相应操作的数据元素集合。它包含三方面的内容，逻辑关系、存储关系及操作。

数据结构分类：

  1. 线性数据结构，如列表、堆栈、队列等。
  2. 非线性数据结构，元素以一对多、多对一和多对多的维度排列，如：树、图形、表格等。

常见数据结构

下面是常见数据结构

  • 数组（Array）：数组是一种聚合数据类型，它是将具有相同类型的若干变量有序地组织在一起的集合。

  • 链表（Linked List）：链表是一种数据元素按照链式存储结构进行存储的数据结构，这种存储结构具有在物理上存在非连续的特点。

  • 栈（Stack）：栈是一种特殊的线性表，它只能在一个表的一个固定端进行数据结点的插入和删除操作。

  • 队列（Queue）：队列和栈类似，也是一种特殊的线性表。和栈不同的是，队列只允许在表的一端进行插入操作，而在另一端进行删除操作。

  • 树（Tree）：树是典型的非线性结构，它是包括，2 个结点的有穷集合 K。

  • 图（Graph）：图是另一种非线性数据结构。在图结构中，数据结点一般称为顶点，而边是顶点的有序偶对。

  • 堆（Heap）：堆是一种特殊的树形数据结构，一般讨论的堆都是二叉堆。

  • 散列表（Hash table）：散列表源自于散列函数(Hash function)，其思想是如果在结构中存在关键字和T相等的记录，那么必定在F(T)的存储位置可以找到该记录，这样就可以不用进行比较操作而直接取得所查记录。

  • Trie：是一种高效的信息检索数据结构。

数组

数组是最简单的数据结构，它是将相同类型的元素存储在连续的内存位置上。数组的特点是查询比较快。

img

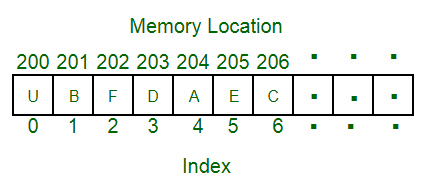
链表

链表和数组一样，链表是一种线性数据结构。与数组不同，链表元素不存储在连续的位置；元素使用指针链接。它的特点是插入元素比较快。

链表

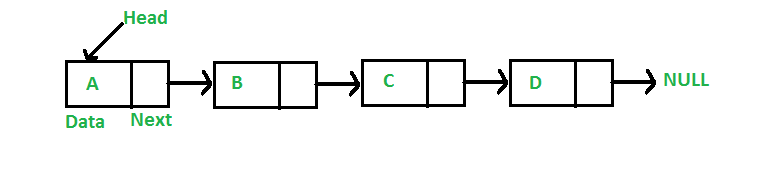
栈

栈是一种线性数据结构，遵循特定的操作执行顺序。顺序可以是 LIFO（后进先出）或 FILO（先进后出）。在栈中，所有插入和删除都只允许在列表的一端。

img

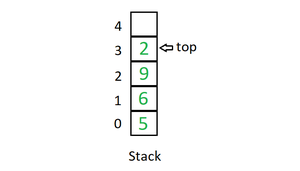
栈中主要执行以下三个基本操作：

  • 初始化（init）：栈为设置为空。
  • 入栈（push）：在栈中添加一个项目。如果堆栈已满，则称其为溢出条件。
  • 出栈（pop）从栈中删除一个元素。这些元素以它们被推送的相反顺序弹出。
  • 返顶（Peek｜top）：返回栈顶部元素。
  • 空判断（isEmpty）：如果栈为空，则返回 true，否则返回 false。

队列

与栈一样，队列是一个线性结构，遵循特定的操作执行顺序。顺序是先进先出 (FIFO)。在队列中，项目在一端插入并从另一端删除。在栈中，我们删除最近添加的元素；在队列中，我们删除最先添加的元素。

img

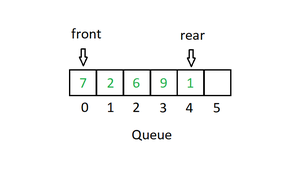
对队列主要进行以下四个基本操作：

  • **入队：**将元素添加到队列中。如果队列已满，则称其为溢出条件。
  • **出队：**从队列中删除一个元素。元素的弹出顺序与它们被推送的顺序相同。如果队列为空，则称其为下溢条件。
  • **Front：**从队列中获取最前面的元素。
  • **Rear：**从队列中获取最后一项。

树

与数组、链表、堆栈和队列是线性数据结构不同，树是分层数据结构。

二叉树

二叉树是一种树数据结构，其中每个节点最多有两个子节点，分别称为左子节点和右子节点。它主要使用链接实现。 二叉树由指向树中最顶层节点的指针表示。如果树为空，则根的值为 NULL。二叉树节点包含以下部分。

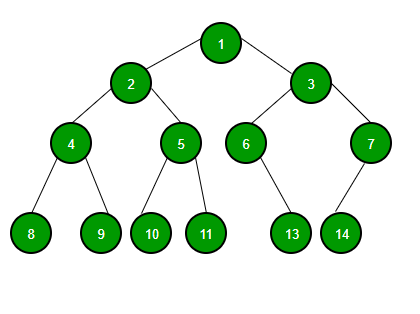
Binary Tree Data Structure

二叉搜索树

二叉搜索树是一种基于节点的二叉树数据结构，具有以下属性：

  • 节点的左子树的节点值始终小于节点。
  • 节点的右子树的节点值始终大于节点。
  • 左右子树也必须是二叉搜索树。
  • 不能有重复的节点。

相当于二叉搜索树在插入时自动维护了元素的有序排列，以方便快速完成搜索、最小值和最大值等操作。如果没有排序，那么我们可能必须比较每个键来搜索给定的键。

200px-Binary_search_tree.svg

红黑树

红黑树是每个节点都带有颜色属性的二叉搜索树，颜色为红色或黑色。在满足二叉查找树条件后，还需满足下面条件：

  • 节点只能是红色或黑色。
  • 根只能是黑色。
  • 所有叶子都是黑色（叶子是NIL节点）。
  • 每个红色节点必须有两个黑色的子节点。（或者说从每个叶子到根的所有路径上不能有两个连续的红色节点。或者说红色节点的父节点和子节点均是黑色的。）
  • 从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点。

An example of a red-black tree

红黑树在实际编程中应用比较广泛，需要重点掌握。这里只是简单阐述其特点，详细请查看《红黑树》。

图

图是由节点和边组成的非线性数据结构。节点有时也称为顶点，边是连接图中任意两个节点的线或弧。定义为：图由一组有限的顶点（或节点）和一组连接一对节点的边组成。

img

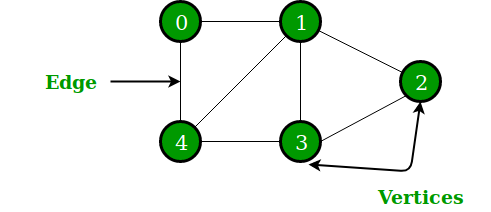
堆

堆是一种特殊的基于树的数据结构，其中树是完全二叉树。通常，堆可以有两种类型：

  1. Max-Heap：在 Max-Heap 中，存在于根节点的键必须是其所有子节点中存在的键中最大的。对于该二叉树中的所有子树，相同的属性必须递归地为真。
  2. 最小堆：在最小堆中，存在于根节点的键必须是其所有子节点中存在的键中的最小值。对于该二叉树中的所有子树，相同的属性必须递归地为真。

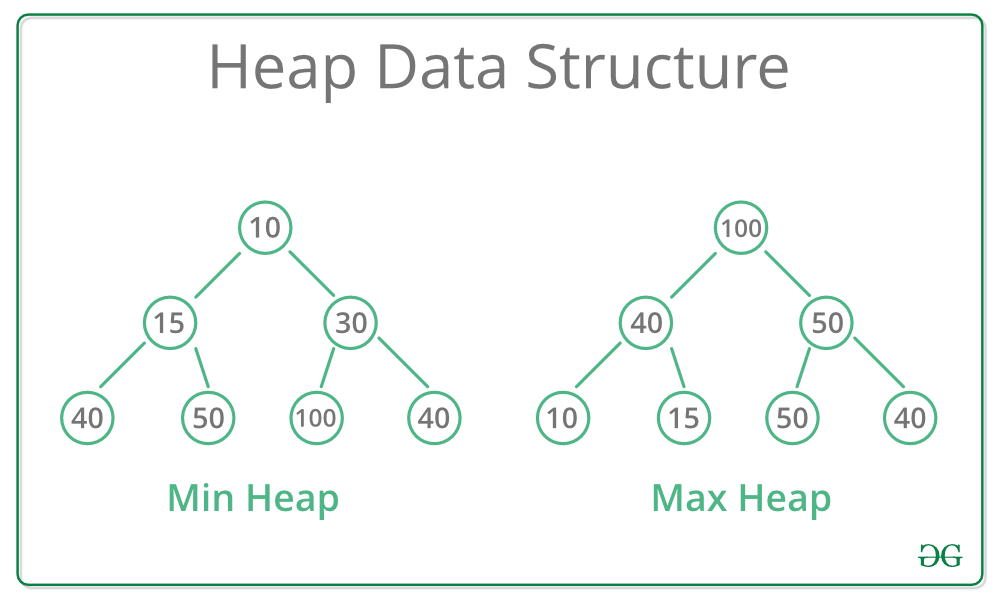
Heap Data Structure

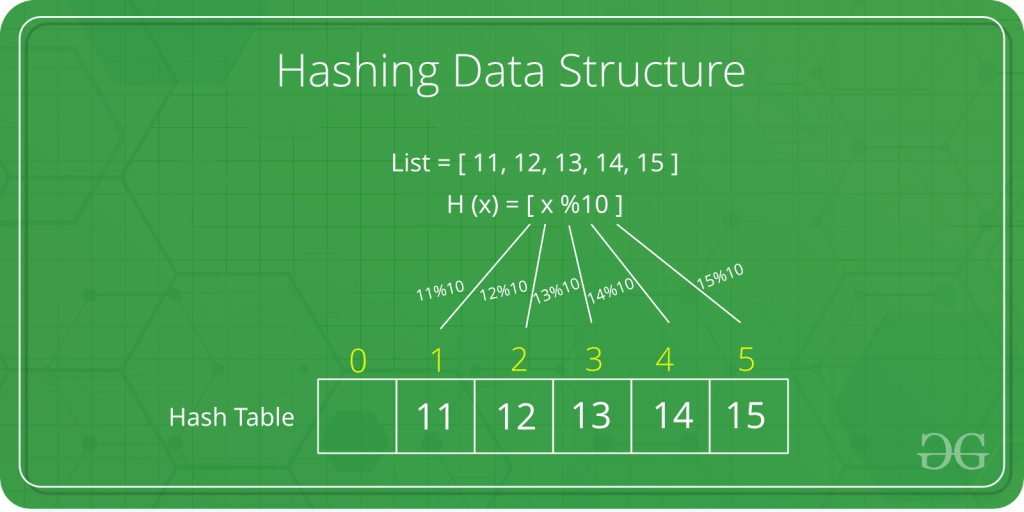
散列表

散列表是一种重要的数据结构，旨在使用称为散列函数的特殊函数，该函数用于将给定值与特定键映射以更快地访问元素。映射的效率取决于所使用的散列函数的效率。 详细请查看散列表。

Hashing Data Structure

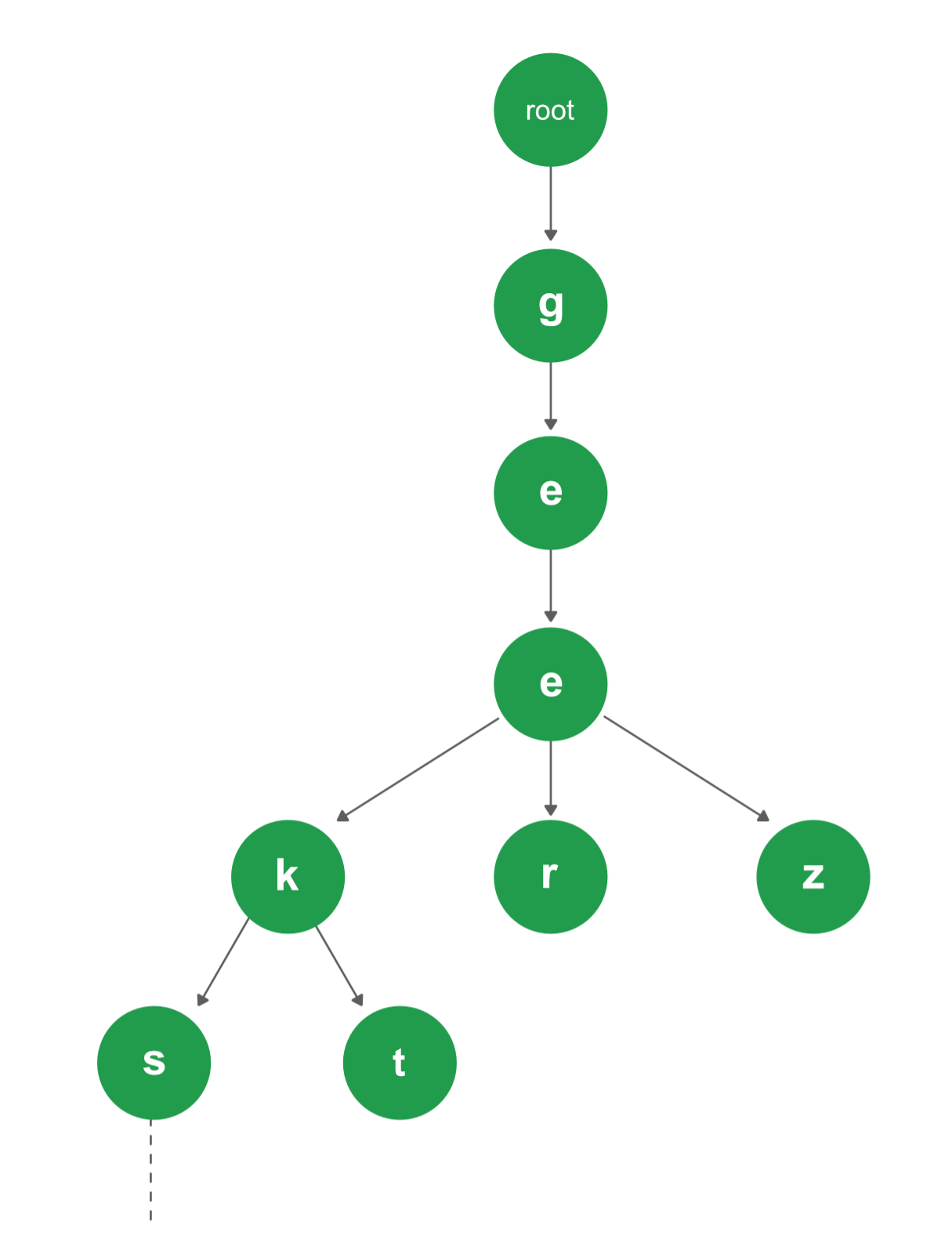
Trie

Trie 是一种高效的信息检索数据结构。使用 Trie，搜索复杂性度可以达到最佳 $O(N)$。在二叉搜索树中，平衡良好的 BST 也需要$O(n \log n)$ ，其中 M 是最大字符串长度，N 是树中键的数量。使用 Trie，我们可以在 $O(M)$ 时间内搜索到键。

img

参考

https://www.geeksforgeeks.org/introduction-to-data-structures

https://en.wikipedia.org/wiki/Data_structure